Abstract
Agroforestry systems by their very mature are complex but are found promoted for many ecological and socio-economic benefits. Experimentation with such systems also inherits many of these complexities. Other than the regular design and analytical options available, the system throws in challenges in the analyses primarily because of varied nature of response variables. Mixture designs and models are especially suited for experimenting with agroforestry systems the latter being mixtures of multiple components. This presentation explores the possibilities of using some of mixture designs and related analytical techniques in conducting agroforestry experiments after a preamble of standard design and analytical methods used in forestry/ agriculture.
Introduction
Agroforestry is a collective name for land-use systems and technologies where woody perennials are grown on the same land-management units as agricultural crops and/or animals, in some form of spatial arrangement or temporal sequence. Nair (~2000) notes that from a purely ecological point, certain types of systems can be identified as characteristic of each major ecological region and lists out the following examples.
Humid/subhumid lowlands – home gardens, plantation crop combinations, multilayer tree gardens, alley cropping and other intercropping systems.
Semi-arid/arid lands– silvipastoral systems, windbreaks/shelter belts, MPTs for fuel/fodder, MPTs on farmlands.
Highlands– soil conservation hedges, silvipastoral combinations, plantation crop systems.
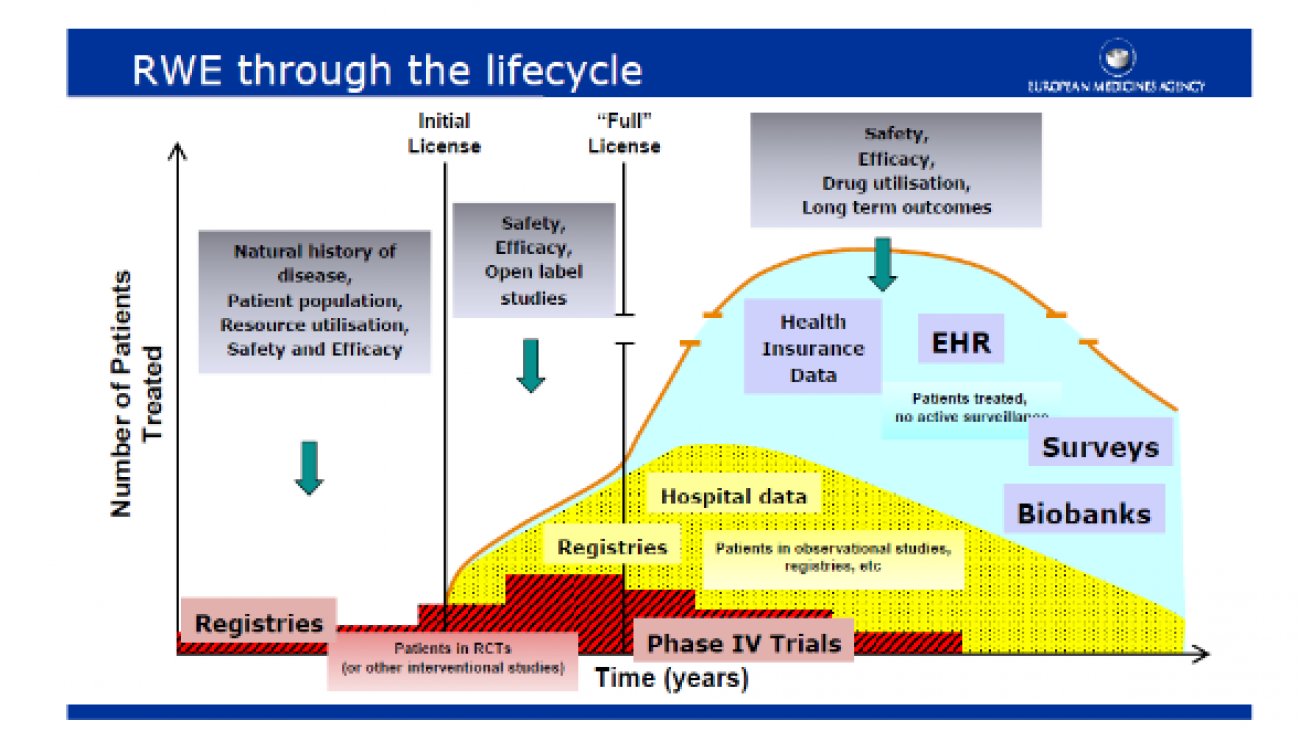
The definition above implies that an agroforestry system normally involves two or more species of plants, at least one of which is a woody perennial, always has two or more outputs, and has the cycle of more than one year. Obviously, there is scope for much inter-component interactions in such systems, positive and/or negative. The system thus is more complex than monocropping and would require special ways of handling these characteristics in respect of design and analysis of experiments. Although the basics of experimentation such as randomization, replication and local control remain the same and many standard designs are applicable with such systems, certain modifications are suggestive to take care of the specialties involved. Hence the standard methodology is described first followed by some special modes of investigations with agroforestry systems.
Standard design and analytical models
The regular designs used for field experiments like randomized complete block design (RCBD), split-plot design and strip-plot design are useful in many situations with agroforestry trials and their use is governed by the particular tree-crop combination under consideration. With large number of factors and levels, fractional factorials or confounded designs come to be of use. Certain systematic designs like fan designs are found suggested for spacing trials to avoid the adjacent occurrence of high and low intensity spacing levels. However, they have their limitations due to lack of randomization of the levels. In all cases, appropriate plot size, block size and borders have to be chosen to enable control of heterogeneity and to avoid edge effects. Subsampling within plots will be required where complete enumeration is not possible within a particular plot.
Characterizing the treatments is of prime importance in agroforestry. The proportion of area occupied by each crop in the mixture at the time of planting is a direct measure in this regard. For instance, a 1:1 mixture could indicate half the area planted under each crop initially. Because the produce from agroforestry systems is of varied nature, they have to be brought to a common ground for any comparison between the treatments. Land Equivalent Ratio (FAO, 1985) is one such index which will show the land area in the system that would be required to produce the same yields as one hectare of intercropping. For a scenario where a total of m crops is intercropped, the land equivalent ratio LER can be calculated as

where m is the number of different crops intercropped, IYi is the yield for i th the crop under intercropping, and SYi is the yield for the i th crop under a sole-crop regime on the same area. For the case of just two crops, the situation could be as follows.

In similar lines, the total biomass per unit area, combined economic returns per unit area are summative measures that can be considered as response variables. The analysis would involve analysis of variance (ANOVA) or analysis of covariance (ANACOV) followed by pairwise comparison or testing of contrasts. The other option is to go for multivariate ANOVA or ANACOV wherein the identity of individual components is retained. The combined analysis takes the form of MANOVA followed by tests based on Hotelling’s T2.
Repeated measurements over time could be a cardinal feature of agroforestry systems for which the analysis would utilize repeated measures model giving information on treatments, the time factor and treatment by time interaction. When several characteristics are involved, it would be better to resort to dimension reduction techniques like principal components analysis followed by ANOVA of the principal components. Agroforestry systems do not generally involve large number of treatments and so may not invoke multiplicity issues in treatment comparisons. One other source of data is that coming from groups of experiments or multilocation trials. The important question here is about the genotype by environment interaction. The same agroforestry system when tried in different soil/climatic zones may behave differently and such information is to be gainfully used. So is the case when several independent investigations are undertaken with similar or different tree-crop combinations. Network meta-analysis will go a long way in synthesizing information from such data sources.
Mixture designs
One grand design proposition for experiments with agroforestry systems is that based on mixture models. A mixture experiment involves mixing various proportions of two or more components to make different compositions of an end product. Mixture components proportions xi are subject to the constraints,

where q is the number of components. As a result, the factor space reduces to regular (q-1) dimensional simplex Sq-1. For q=2 it is a straight line x1+x2=1 and for q=3 it is an equilateral triangle. One related question is how to compute the proportions under different crops in an agroforestry system. The one based on planted area seems to qualify for the same.
Scheffe (1958, 1963) introduced the {q,m} simplex lattice designs and simplex-centroid designs. The {q,m} simplex lattice designs are characterized by the symmetric arrangements of points within the experimental region and a well-chosen polynomial equation to represent the response surface over the entire simplex region. The polynomial has exactly as many parameters as there are number of points in the associated simplex lattice design.
The {q,m} simplex lattice design given by Scheffe (1958) consists of q+m-1Cm points where each component proportion takes (m+1) equally spaced values xi=0,1/m, 2/m,…,1; i=1,2,…,q, ranging between 0 and 1 and all possible mixtures with these component proportions are used.
For example: a {3,2} simplex lattice will consist of 3+2-1C2 i.e. 4C2=6 points. Each xi can take m+1=3 possible values xi=0, 1⁄2,1 with which the possible design points are (1,0,0), (0,1,0), (0,0,1), (1⁄2, 1⁄2, 0), (0, 1⁄2, 1⁄2), (1⁄2, 0, 1⁄2).

Scheffe (1963) gave simplex centroid designs which consists of 2q -1 points with q permutations of (1,0,0,…, 0) (i.e., q pure blends), (qC2) permutations of (1⁄2,1⁄2,0,…0) (i.e. (qC2) binary blends),…, and the overall centroid (1/q, 1/q,…, 1/q) (i.e. the q-nary blend).
For q=3, the simplex centroid design consists of seven points (1,0,0), (0,1,0), (0,0,1), (1⁄2, 1⁄2, 0), (0, 1⁄2, 1⁄2), (1⁄2, 0, 1⁄2) and (1/3,1/3,1/3).

The (q,m} simplex-lattice and q-component simplex-centroid designs are boundary designs in that,
with the exception of the overall centroid, the points of these designs are positioned on the
boundaries (vertices, edges, faces, etc.) of the simplex factor space. Axial designs on the other
hand, are designed to consist mainly of complete mixture or q-component blends where most of
the points are positioned inside the simplex. Axial designs have been recommended for use when
component effects are to be measured and in screening experiments, particularly when first-degree
models are to be fitted. Designs with points lying on the axis of components, that is imaginary line
extending the base points xi=0, xj=1/(q-1) v i≠j to the vertex where xi=1, xj=0 v i≠j, are called axial
designs.

Mixture models
Data from mixture designs are analyzed through mixture models involving Scheffe’s canonical polynomials. Scheffe (1958) introduced canonical polynomials to be used with his simplex lattice designs. These polynomials are obtained by modifying the usual polynomial model in xi by using the restriction Σxi=1.
The number of terms in {q,m} polynomial or canonical polynomial is (q+m-1Cm) and this number is equal to the number of points that make up the associated {q,m} simplex lattice design. For example, for m=1 the linear canonical model is
η = ∑ βixi
The number of terms in equation (2) is q, which is the number of points in the {q,1} lattice. For m=2, the second-degree canonical polynomial is
η = ∑ βixi + ∑∑ βijxixj
The number of terms in (1.3) is q+q(q-1) /2 = q(q+1) /2.
The full cubic canonical polynomial or (q,3) polynomial is

A simpler formula for a special case of the cubic polynomial is the special cubic polynomial

the number of terms in equation (5) is q(q2 + 5)/6.
For each of the above models, formulae for estimating the parameters and their variances are available in Cornell (2002).
The analysis of variance table takes the regular form of a regression model:
| Source of Variation | Degrees of Freedom | Sum of Squares | Mean squares |
|---|---|---|---|
| Regression (fitted model) | p-1 |  |
MSR=SSR/(p-1) |
| Residual | N-p |  |
MSE=SSE/(N-p) |
| Total | N-1 |  |
The results of mixture experiments are usually depicted in the form of a contour plot which shows the intensity of response across the factor space. The following graph shows the CO2 adsorption rates for MCM-41 synthesized using three types of surfactants (Costa et al, 2015). The optimal mixture has been C17: C19 in equal proportion giving a CO2 adsorption rate of 0.62 g CO2/g adsorbent.

Process variables
In some mixture experiments, the response depends not only on the proportion of the components present in the mixture but also on the processing conditions. Process variables are factors in an experiment that do not form any portion of the mixture but whose levels when changed could affect the blending properties of the ingredients. The models involve both mixture variables and process variables. For instance, in agroforestry experiments, the same mixture could occur at different planting densities or fertilizer levels.
The methodology used to construct mixture designs involving process variables is composition of two smaller designs, one being a mixture designs for the mixture components only and the other being factorial/fractional factorial design for the process variables. For example, with two mixture components having the proportions x1 and x2, suppose there are also two process variables, denoted by z1 and z2 and each process variable is to be studied at two levels. If a three-term quadratic model in x1 and x2 is to be fitted to data collected at the point of a {2,2} simplex lattice, the combined {2,2} lattice x 22 factorial arrangement can be used.

For instance, the three terms quadratic model in two components

when combined with the four-term main and interaction effect model in z1 and z1

produces the 12-term combined model

where

These models help us also understand the interactions between process variables and mixture components.
Conclusions
Considerable developments have taken place in this field and it is open for agroforestry researchers to adopt a suitable design and analytical technique for his/her studies. However, the real advantage of mixture models is, having tried a few pure or combination mixtures in reality, the models have the capability to predict the responses associated with any level of mixing across the range experimentation or factor space.